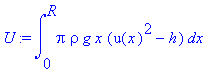
> restart;
> U:=int(pi*rho*g*(x*(u(x)^2-h)),x=0..R);
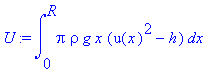
> K:=-int(pi*omega^2*rho*x^3*(u(x)-h),x=0..R);
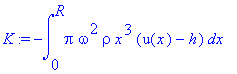
> V:=int(2*pi*u(x)*x,x=0..R);
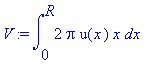
> E:=K+U+lambda*V;
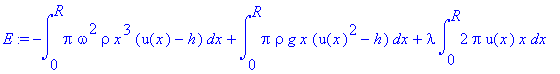
> t1:=subs({u(x)=a1,diff(u(x),x)=a2},E);
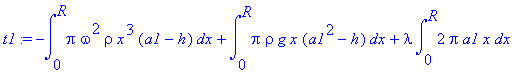
> t2:=subs(R=x,diff(t1,R));
![]()
> t3:=subs({a1=u(x),a2=diff(u(x),x)},diff(t2,a1))-diff(subs({a1=u(x),a2=diff(u(x),x)},diff(t2,a2)),x);
![]()
> u1:=solve(t3,u(x));
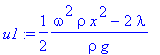
> constraint:=h0*R^2*pi=V;
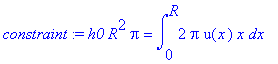
> subs(u(x)=u1,constraint);
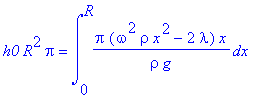
> solve(%,lambda);
![]()
> lambda1:=%;
![]()
> u2:=subs(lambda=lambda1,u1);
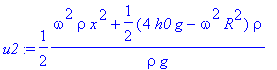
> simplify(%);
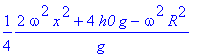
>
>