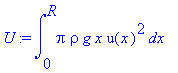
> restart;

> U:=int(pi*rho*g*(x*(u(x)^2)),x=0..R);

>

>

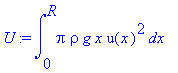
> K:=-int(pi*omega^2*rho*x^3*(u(x)),x=0..R);

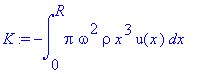
> V:=int(2*pi*u(x)*x,x=0..R);

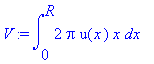
> ST:=sigma*int(2*pi*x*u(x)*sqrt(1+diff(u(x),x)^2),x=0..R);

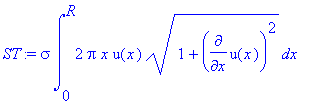
> E:=K+U+ST+lambda*V;

>

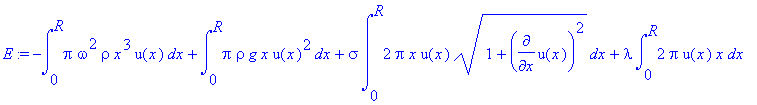
> constraint:=pi*R^2*h0=V;

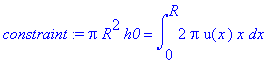
> eq1:=subs(R=x,diff(E,R));

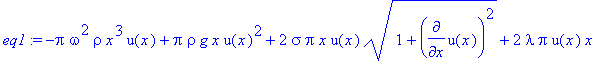
> eq2:=subs({u(x)=a1,diff(u(x),x)=a2},eq1);

> eq3:=subs({a1=u(x),a2=diff(u(x),x)},diff(eq2,a1))-diff(subs({a1=u(x),a2=diff(u(x),x)},diff(eq2,a2)),x)=0;

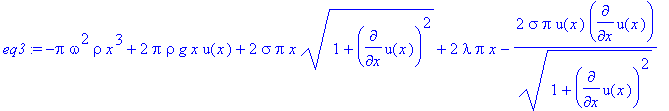
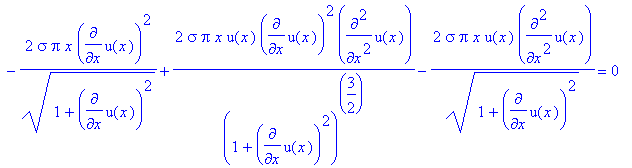
# Using the inch/pound/second system

> eq4:=subs({sigma=0.15432358,pi=3.141592,rho=0.036127292,g=386.08858},eq3);

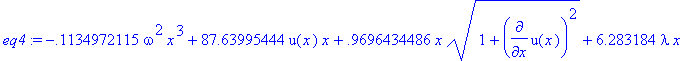
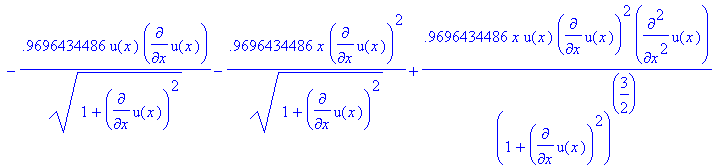
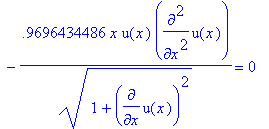
> R:=1.909859317; h0:=3.3750;

>

> eq5:=eq4;

>

>

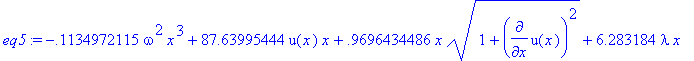
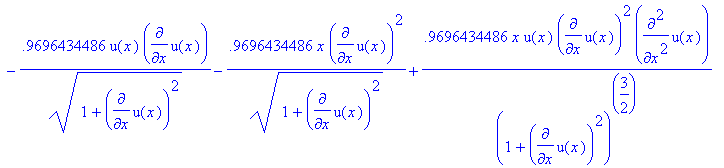
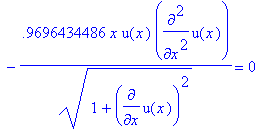
> infolevel[dsolve]:=3;

>

> Order:=6;

> a:=array(0..Order);

# a[1] = 0 because we require that the first derivative of u at 0 is 0

> a[1]:=0;

>

> u_s(x):=sum(a[n]*x^n,n=0..Order);

> eq6:=subs({u(x)=u_s(x)},eq5);

> eq7:=simplify(eq6);

>

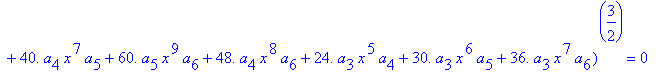
> eq8:=taylor(lhs(eq7),x);

> eq9:=convert(eq8, polynom);

> s:=coeffs(eq9,x);

> eq9:=map(x->x=0,{s});

Error, (in solve) invalid arguments

>

> eqns:=solve(eq9,{seq(a[i],i=2..Order)});

>

>

> u_1(x):=subs(eqns,sum(a[n]*x^n,n=0..Order));

#Trial 1, rotational speed = 6.86 rad/sec

# a[0] is found from experimental data

> u_a(x):=subs({a[0]=2.6250,omega=6.860570959},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

>

> subs(x=n58,u_f(x));

>

> plot(u_f(x),x=-R..R);

Trial #2, rotational speed = 9.02 rad/sec

> u_a(x):=subs({a[0]=2.1250,omega=9.017534469
},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

>

> plot(u_f(x),x=-R..R);

Trial #3: rotational speed = 8.31 rad/sec

> u_a(x):=subs({a[0]=2.4375,omega=8.31089566},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

>

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

Trial #4: rotational speed = 6.89 rad/sec

> u_a(x):=subs({omega=6.889385357,a[0]=2.6250},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

Trial #5: rotational speed = 8.89 rad/sec

> u_a(x):=subs({omega=8.888555735,a[0]=2.2500},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

Trial #6: rotational speed = 9.21 rad/sec

> u_a(x):=subs({omega=9.205514113,a[0]=2.8125},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

Trial #7: rotational speed = 10.15 rad/sec

> u_a(x):=subs({omega=10.14678445,a[0]=2.1875},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

Trial #8: rotational speed = 8.56 rad/sec

> u_a(x):=subs({omega=8.558728285,a[0]=2.0000},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

>

Trial #9: rotational speed =9.91 rad/sec

> u_a(x):=subs({omega=9.913521036,a[0]=1.6250},u_1(x));

> # Get a lambda that fits the constraint

> lambda_optimal:=max(fsolve(2*int(u_a(x)*x,x=0..R)-R^2*h0=0,lambda));

> u_f(x):=subs(lambda=lambda_optimal,u_a(x));

> subs(x=n58,u_f(x));

> plot(u_f(x),x=-R..R);

>

>

>

>

>

>

>

>