Calculations

Placing a diagram of a cross-section of the rotating jar and water in a Cartesian plane as shown,

x₀

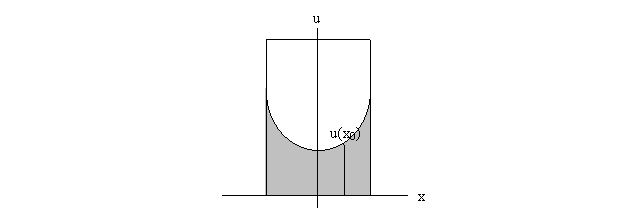
our objective is to derive a function u(x) that models the shape of the water by giving the height of the surface of the water above a given point on the x-axis. We can derive such a function by calculating the total energy from the system and minimizing it using the Euler-Lagrange equation.

We consider only the rotational kinetic and gravitational potential energy of the system, assuming all other sources of energy to be negligible because they are relatively weak in this system (we will later examine the effects of factoring surface tension into our calculations). From mechanics of physical systems, we have the equations

,

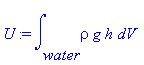
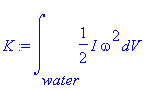where K is the rotational kinetic energy of the system, U is the gravitational potential energy, I is the moment of inertial of the water, ω is the rotational velocity the fluid (constant), ρ is the density of the water (constant), g is the force of gravity on the water (constant), and h is the height of each infinitesimally small cube of water dV above the bottom of the jar. We find the total kinetic and potential energies of the system by integrating over all cubes dV of water.

We consider our kinetic energy equation first. Since ω is constant throughout the water, we can place it outside our integral, leaving us to calculate I. By the formula for moment of inertia, the value of I for each element dV of water is I = ρx², where x is the distance of dV from the axis of rotation (the u-axis in the diagram above), so our total moment of inertia is

,

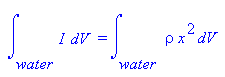and our total kinetic energy is

.

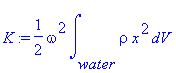However, the integral in this form is too difficult to solve, in part because we do not have clear bounds and in part because we have not found a way to include u(x) into the equation. We solve this problem by changing the variables from Cartesian to cylindrical coordinates, giving us

,

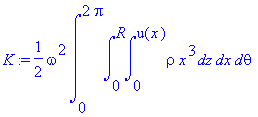where R is the radius of the cylinder, x is the horizontal distance of each element dV from the axis of rotation (the u-axis on the diagram at top), z is the vertical distance of each element from the bottom of the jar, and θ is the angle of dV from a fixed Cartesian plane that intersects the axis of rotation.

So we now have an integral that, if evaluated, may be solved for u (x) but since kinetic energy is only part of the overall equation (total energy) that we wish to derive, we will hold off and solve it later as part of this larger equation.

We now consider our potential energy equation. We have

.

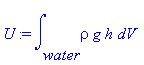
We convert the variables to cylindrical coordinates following the same logic as our kinetic energy equation:

.

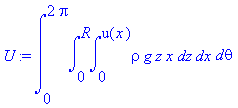So our total system energy is

.

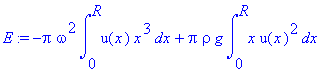Kinetic energy is negative because, by the law of the conservation of energy, kinetic and potential energy have an inverse relationship.

Note, however, that we have a constraint in the motion of the water inside the jar. Assuming that compression forces on the water are negligible and observing that no water is lost during the system’s rotation, our volume remains fixed. Thus, our calculations are affected by the constraint

,

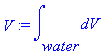where V is the total volume of the water. By the shell method,

.

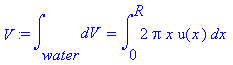We then factor this limitation into our total energy equation using a Lagrange multiplier λ, so we have

.

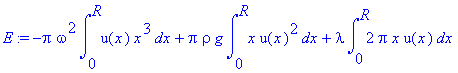Following the procedure for implementing the Euler-Lagrange equation on an integrated function, we let F(z, p) equal the integrand of the energy equation—that is,

,

where z = u(x) and p = u’(x) (note that this is not the same z used in the triple integrals above)—which we substitute into the Euler-Lagrange formula

to get

.

So we can solve for u(x) to get

.

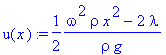However, we still need to solve for λ since it’s the only parameter in the equation, so we examine the function associated with λ, which in this case is our constraint function

,

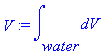which states that the volume of water within the jar is constant for different rotational velocities. If we allow the volume of water when the system is at rest to be πR²h₀, where R is the radius of the cylinder and h₀ is height of the standing water from the bottom of the jar, then

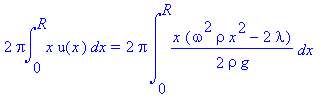
πR²h_{0 =}

.

Evaluating the integral and solving for λ gives us

,

so our final value of u(x) is

.
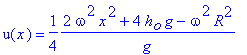