Second Question

We now consider the effect on our calculations when we factor in surface tension.

The formula for the surface tension of a liquid whose surface may be defined by the curve u(x) is

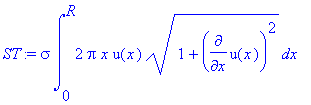
where σ is a constant which is a function for temperature. For water, the value is σ = 0.07 N/m.

Surface tension is a source of energy in this system, so we add it into our total energy equation, giving us

.

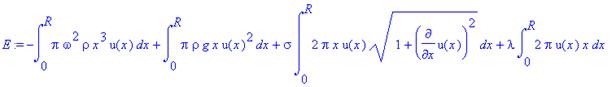As before, we minimize our function by substituting the integrand

,

where z = u(x) and p=u’(x), into the Euler-Lagrange equation

,

giving us

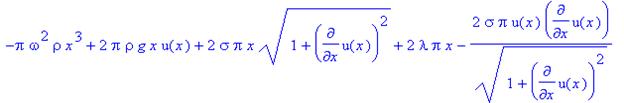
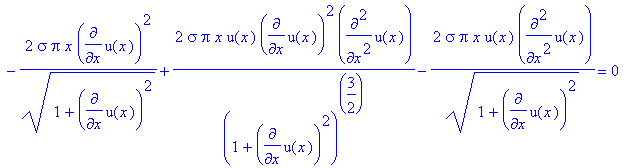
after we substitute u(x) and u’(x) back in for z and p.

However, we cannot solve the equation for u(x) in this form because it is nonlinear, so we’re not guaranteed a long-term numeric solution. We solve this problem by approximating u(x) with a power series

,

which, substituting into our solution from the Euler-Lagrange equation, gives us

.

We can simplyify this, but the result is an excessively long equation. We can simplify this equation by taking the fifth order Taylor approximation (see Appendix A).

But now we have seven unknowns—the values a₀ through a₆—which we need to solve for. We start by observing that since the original Euler Lagrange equation is equal to zero, then so is the Taylor approximation. For this to be true, the seven coefficients in the Taylor approximation must be equal to zero. If we set each coefficient equal to zero, then we have seven equations, which we can use to start solving for our values a₀ through a₆. We know that a₁ = 0 because a₁ equals the initial condition (u’(0)) of u’(x) by definition, and u’(0) = 0 because the tangent at u(0) has 0 slope (see the diagram below).

Taking our remaining values a₀ and a₂ through a₆, we can solve for the latter to get

,

which we then substitute back into our power series to give us an approximation of u(x):

.

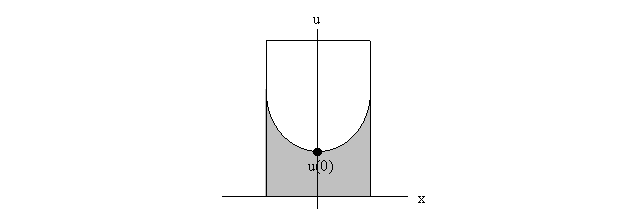
Our coefficients are in terms of a₀, and we cannot solve them any further. Thus, we must rely on our experimental data to satisfy the value of a₀. For each trial, we set a₀ equal to the experimental value closest to 0 because a₀ is the initial condition u(0) by definition, and u(0) should theoretically fall at the lowest point of the rotating water, as seen below on the diagram of a cross section of the system.

A complete analysis of the effect of surface tension on our calculations is included in the Data Analysis and Conclusions section.